
Was versteht man unter Fähigkeit und was bedeuten cp und cpk ?
Ein Beitrag von Dr. Uwe-Klaus Jarosch, August 2025
Seit nunmehr 100 Jahren ist erwiesen, dass für sich wiederholende Abläufe mit statistischen Betrachtungen eine Aussage möglich ist, wie gut das Ergebnis dieses Ablaufs, dieses Prozesses ist.
Der Statistiker Dr. Walter Andrew Shewhart gilt als der „Erfinder“ der Statistischen Prozess-Lenkung (SPC). Im Jahr 1925 erarbeitete er erstmals Qualitäts-Regelkarten und ermöglichte damit, das Qualitätsniveau zu messen und aus diesen Daten gezielt zu verbessern.
Aus der Mathematik waren die wesentlichen Zusammenhänge und Begriffe bekannt. Shewhart hat sie erstmalig auf konkreten Fertigungsprozesse angewendet.
Dabei hat er erkannt, dass es ausreicht, in regelmäßigen Abständen eine repräsentative Stichprobe zu untersuchen, um zu einer gesicherten Aussage über das Qualitätsniveau zu kommen.
Heute verwenden wir diese Statistik an vielen Stellen.
Das Ergebnis der Berechnungen wird vielfach auf eine oder zwei Kennzahlen, Fähigkeits-Indizes, zusammengefasst.
Die beiden wesentlichen Kennzahlen sind cp und cpk.
Diese Abkürzungen stehen für englisch capability of process.
Das k in cpk wird auf das japanische Wort Katayori = Bias, Verschiebung zurückgeführt. Es bezeichnet den „strengeren“ Index.
Es finden sich in den praktischen Anwendungen weitere Kürzel, z.B. pp (process performance), cm (machine capability),
die aber sehr ähnlich bzw. identisch bestimmt werden.
Normalverteilung = Glockenkurve
Die erste Näherung um die Verteilung von Messwerten um den ermittelten Mittelwert zu beschreiben, ist die Gauss’sche Normalverteilung. Ihr kennt sie als Glockenkurve. Früher war diese Verteilungsfunktion auf jedem 10-Mark-Schein zusammen mit dem Portrait von Gauss zu sehen.
Im folgenden Bild ist rechts eine solche Glockenkurve dargestellt.
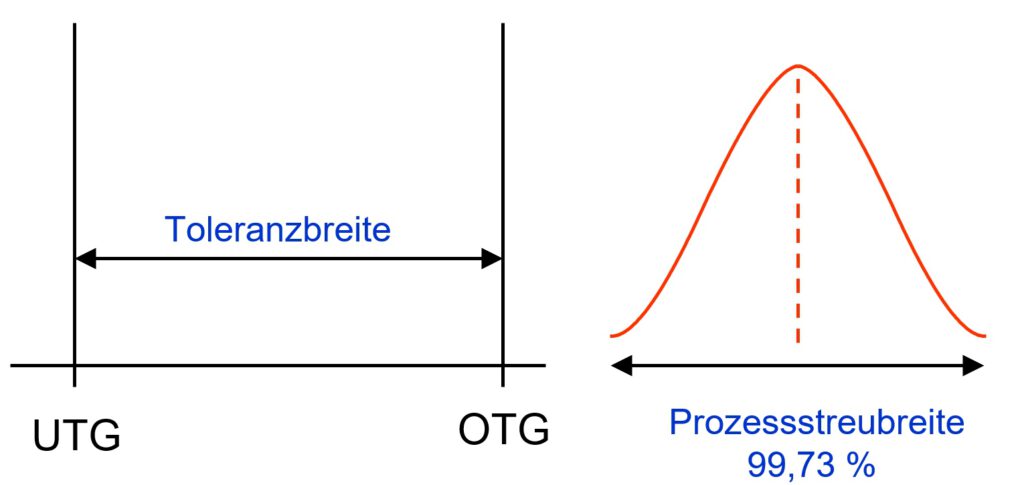
Um diese Darstellung zu verstehen, benötigen wir 2 Angaben:
Zum einen (links) müssen wir etwas über die Toleranzbreite wissen. Die Toleranzbreite ergibt sich aus dem Abstand zwischen der oberen Toleranzgrenze (OTG) und der unteren Toleranzgrenze (UTG).
TB = OTG – UTG.
Zum anderen haben wir die Messwerte. Die Messwerte haben irgendeinen Wert und wir erwarten, dass dieser Wert zwischen OTG und UTG liegt. Die horizontale Achse dieser Grafik wird in feine Abschnitte unterteilt und dann wird die orangene Linie in der Höhe gezeichnet, die der Anzahl der Messwert in diese Abschnitt entspricht. Bei einer natürlichen Verteilung, wie sie die Glockenkurve wiedergibt, sind in der Mitte der Verteilung die meisten Zählungen, daher dort die Spitze der Kurve.
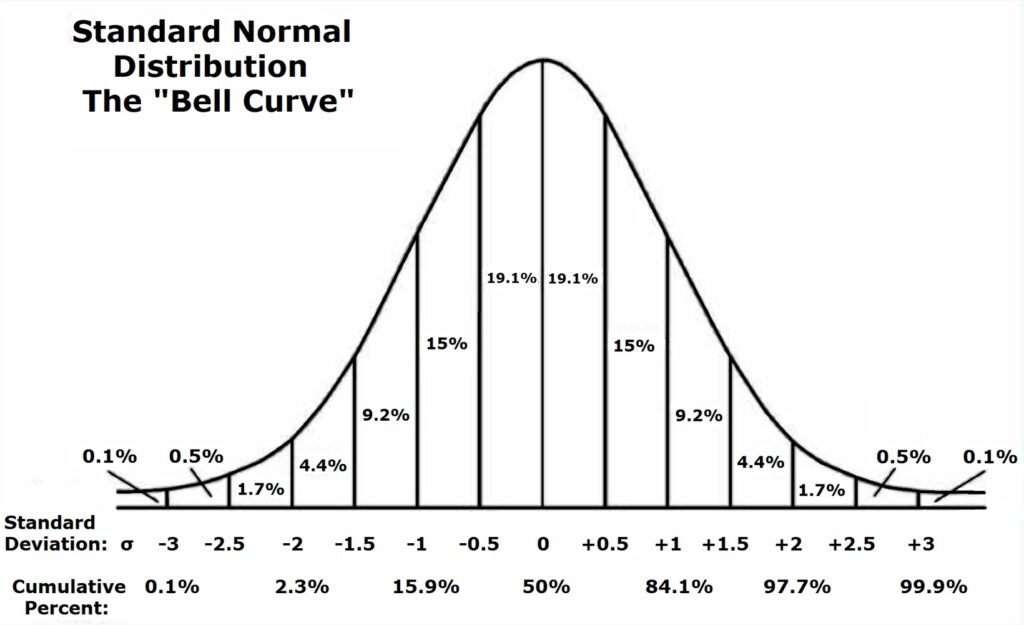
In der nachfolgenden Grafik sehen wir auch eine Messwertverteilung. Für diesen Kurvenverlauf können wir eine Standardabweichung ausrechnen.
In dieser zweiten Verteilungsfunktion sind jetzt vertikale Linien eingezeichnet, wenn wir jeweils um 1/2 Standardabweichung weiter von der Mitte nach außen wandern.
Zudem ist aufgeschrieben, wie viele % aller Messwerte in diesem Abschnitt zu finden sind.
Bis zu den beiden Linien für 3x Standardabweichung Sigma kommen wir auf 99,8%.
Jetzt müssen wir Prozessstreubreite und Toleranz übereinanderlegen.
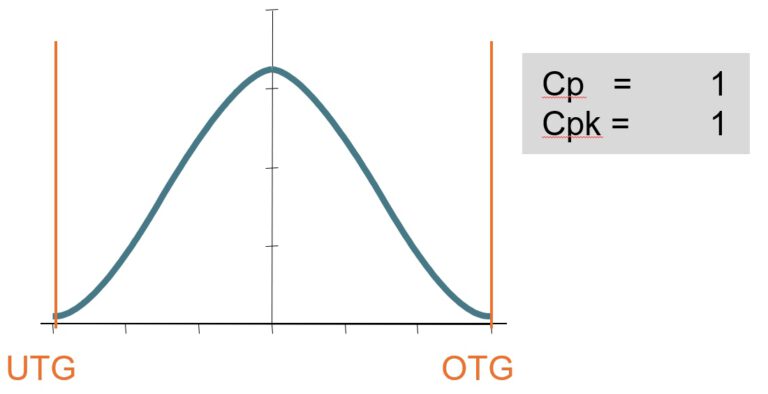
cp = cpk = 1,0.
Wenn 99,8% innerhalb der Grenzen liegen, dann sind 0,2% außerhalb. Für die Qualität bedeutet „außerhalb der Spezifikationsgrenze“ : dieser Messwert und das zugehörige Teil oder der gemessene Zustand ist NiO – Nicht in Ordnung.
Hochgerechnet bedeuten 0,2% 200 NiO-Teile, NiO-Zustände auf 1 Million Messungen.
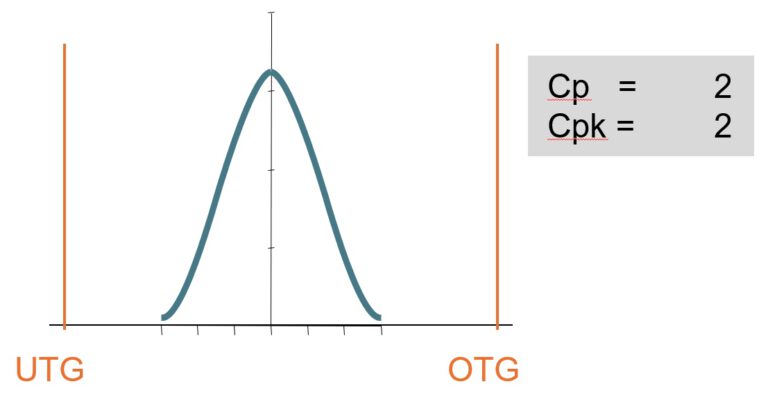
cp = cpk = 2,0.
Stimmen cp und cpk überein, dann ist die Verteilung genau im Zentrum des Toleranzbereichs.
Aber die Verteilung ist viel enger um das Zentrum konzentriert. Von der Mitte bis zu den Toleranzgrenzen würden wir die Standardabweichung Sigma jeweils 6x hineinbekommen.
Die Kurve der Verteilung würde nicht bei 3 Sigma aufhören, sondern sich nach außen unendlich weit fortsetzen, aber eben mit ganz ganz kleinen Werten.
Der aller-überwiegende Teil der verbleibenden 0,2% würde jetzt innerhalb des Toleranzbereichs liegen.
Die genauen NiO-Anteile findet ihr weiter unten.
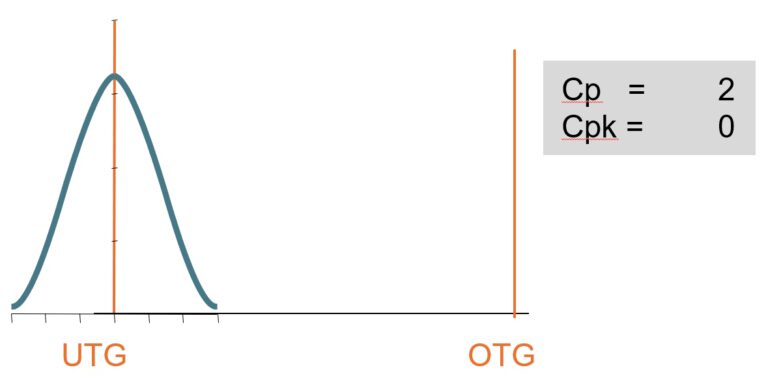
Was sagt cp ?
cp zeigt die Breite der Verteilung
Die Rechnung ist einfach: Toleranzbreite geteilt durch 6x Sigma.
Egal, wo diese Verteilung liegt, das Ergebnis berücksichtigt nur die Breite und macht eine Aussage zur Streuung.

Anders bei cpk.
cpk zeigt statistisch erwartete Anzahl von NIOs
Die Berechnungsformel für cpk schaut sich den Abstand von der Mitte der Verteilungsfunktion zur näher liegenden Toleranzgrenze an.
Das bedeutet, dass eine Verschiebung aus der Mitte den cpk-Wert immer schlechter werden lässt.
Ein guter cpk-Wert bedeutet, dass die Verteilungsfunktion steil ist, eine geringe Streuung aufweist UND gut zentriert zwischen den Toleranzgrenzen liegt.
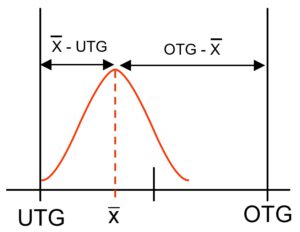
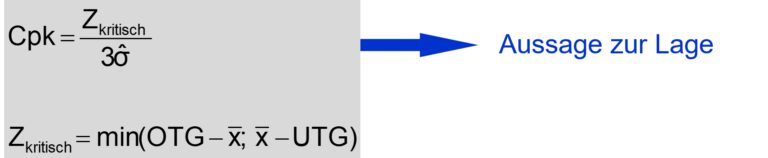
Es wird immer enger
Für cpk=1,0 hatten wir einen Rest von bis zu 200 NiO je 1 Million Messungen (PPM) ermittelt.
Bei cpk = 1,33 liegt der erwartete Restfehler bei bis zu 63 Parts per million,
bei cpk = 1,67 liegen wir bei ca. 0,6 PPM
und bei cpk = 2,0 ist die Erwartung 0,002 PPM, also real wirklich nichts mehr.
Warum reden wir von „bis zu“ und nicht von genauen Werten?
Wenn wir exakt in der Mitte liegen und symmetrisch zu größeren wie zu kleineren Werten hin abfallen, dann treffen diese Zahlen genau zu.
Liegt ein Verschiebung aus dem Zentrum vor, so ist nur einer der beiden Seiten der Verteilung betrachtet, auf der anderen Seite liegen mehr i.O.-Werte vor, sodass in Summe weniger NIOs gezählt werden.
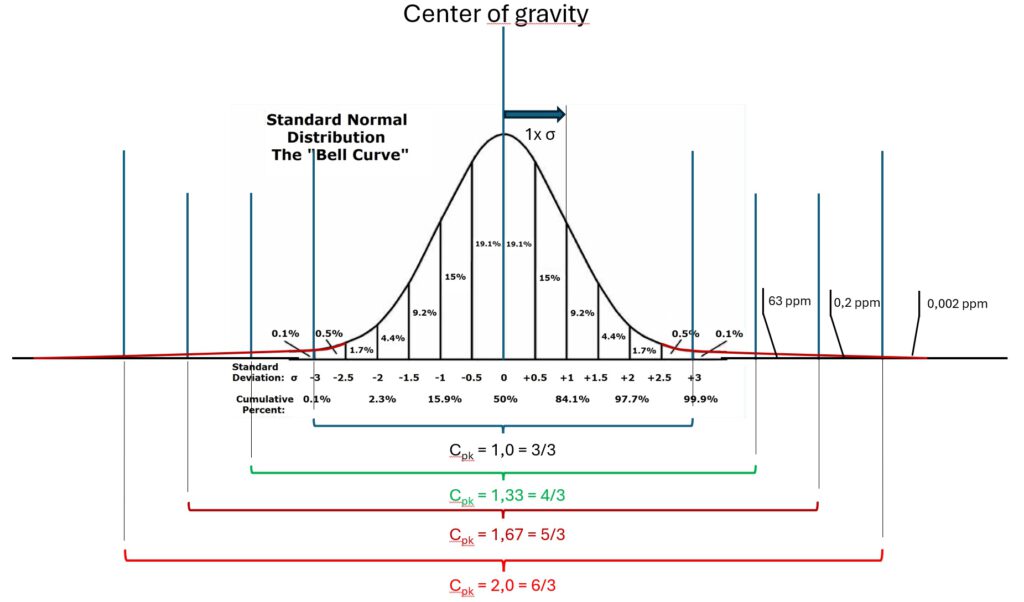
Aber je höher der erwartete Wert für cpk, aber auch für cp liegt, um so anstrengender wird es, das im laufenden Prozess und auf Dauer zu erfüllen.
Automatisierung hilft.
100%-Prüfung hilft nicht, wenn die Teile schlecht sind. Dann sind so viele NiO in der Nähe der Grenzen, dass die Statistik keine akzeptablen Fähigkeitsindizes mehr ausweisen kann. Die Verteilung mag immer noch einer Gauss-Glocke ähneln, aber die Grenzen liegen viel zu nahe am Zentrum der Verteilung. Oder anders herum argumentiert: Der Prozess ist viel zu schlecht, nicht fähig, um innerhalb der Vorgaben sicher gute Teile zu produzieren.
Der Königsweg sind geregelte Prozesse: Es wird regelmäßig gemessen, die Messwerte liegen innerhalb der Toleranz, aber die gemittelte Abweichung mehrerer Werte wird genutzt, um die Prozessparameter so zu verändern, dass das Prozessergebnis wieder genau in die Mitte wandert und eng um die Mitte verteilt bleibt.
Fazits:
- cp und cpk werden aus der Näherung einer idealen Gauss’schen Glockenkurve abgeleitet. Sie sind daher nur erste Näherungen realer Verteilungsfunktionen.
- cp und cpk sind zunächst für zweiseitig begrenzte Merkmale mit symmetrischer Verteilung der Werte zum Mittelwert anwendbar.
- Für beide Fähigkeits-Indizes ist die Kenntnis über die Toleranzgrenzen und über die Standardabweichung aus allen betrachteten Werten nötig.
- cp bewertet die „Breite“ der Verteilungskurve im Verhältnis zur Toleranzbreite. Wo die Werte genau liegen ist unerheblich. cp ist immer eine positive Zahl.
- cpk bewertet ebenfalls die Breite der Verteilungsfunktion, allerdings wird mit dem Abstand zwischen dem Mittelwert der Verteilung und der näher liegenden Toleranzgrenze gerechnet. Je weiter der Mittelwert aus dem Zentrum zwischen den Toleranzgrenzen rückt, um so kleiner = schlechter wird er. cpk kann negativ werden. Dann liegt der Mittelwert nicht mehr zwischen den Toleranzgrenzen.
Bleiben sie neugierig.
Uwe Jarosch